What is Clustering?
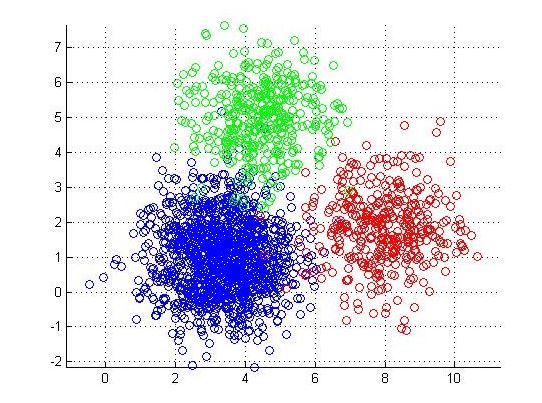
Clustering is the process of partitioning a group of data points into a small number of clusters.
K-means Clustering
K-means clustering (MacQueen, 1967) is a method commonly used to automatically partition a data set into k groups. It is unsupervised learning algorithm.

K-means Objective
• The objective of k-means is to minimize the total sum of the squared distance of every point to its corresponding cluster centroid. Given a set of observations (x1, x2, …, xn), where each observation is a d-dimensional real vector, k-means clustering aims to partition the n observations into k (? n) sets S = {S1, S2, …, Sk} so as to minimize the within-cluster sum of squares where µi is the mean of points in Si.

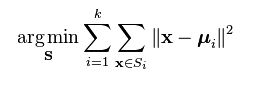
• Finding the global optimum is NP-hard.
• The k-means algorithm is guaranteed to converge a local optimum.

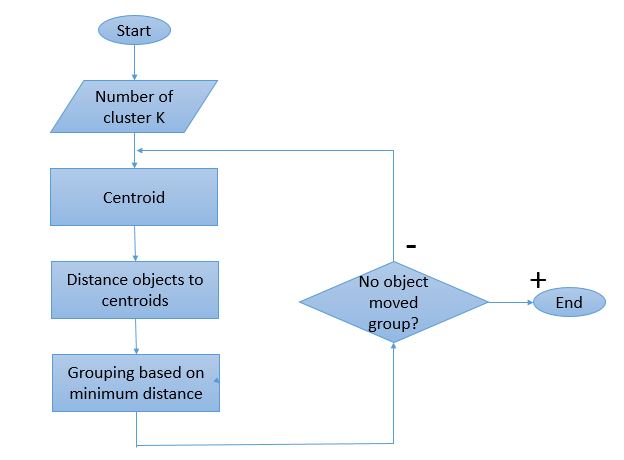
The algorithm is composed of the following steps:
Step 1. Place K points into the space represented by the objects that are being clustered. These points represent initial group centroids.
Step 2. Assign each object to the group that has the closest centroid.
Step 3. When all objects have been assigned, recalculate the positions of the K centroids.
Repeat Steps 2 and 3 until the centroids no longer move. This produces a separation of the objects into groups from which the metric to be minimized can be calculated.

Process flow of K-means Clustering algorithm 

Step by step for performing the K-means clustering on Text data

For performing the K-means clustering on Text data required some special packages, which need to install text mining package to load a library called tm. In this process data is stored in .csv file is used.
Step 1: Reading the Data from .csv file.
Step 2: Create a corpus from the collection of text files.
Step 3: Performing the Data processing transformation on the text data.
1. Transform characters to lower case.
2. Converting to Plain Text Document
3. Remove punctuation marks.
4. Remove digits from the documents.
5. Remove from the documents words which we find redundant for text mining (e.g. pronouns, conjunctions). We set this words as stopwords(“english”) which is a built-in list for English language.
6. Remove extra whitespaces from the documents.
Step 4: Now create the “Term document matrix”. It describes the frequency of each term in   each document in the corpus.
Step 4: Perform the distance euclidean distance and calculating the distance matrix
Step 5: Apply k-means algorithm and store the clustering result in variable. The cluster number is set to 6.
Step 6: Display the results.

Implementation of K-means clustering in R code

library(tm)
Sample_data<-read.csv('Path of csv file')
data_frame<- do.call('rbind', lapply(Sample_data, as.data.frame))
myCorpus <- Corpus(VectorSource(data_frame))
myCorpus <- tm_map(myCorpus, tolower)
myCorpus <- tm_map(myCorpus, PlainTextDocument)
myCorpus<- tm_map(myCorpus,removePunctuation)
myCorpus <- tm_map(myCorpus, removeNumbers)
myCorpus <- tm_map(myCorpus, removeWords,stopwords("english"))
myCorpus <- tm_map(myCorpus, stripWhitespace)
dtm <- TermDocumentMatrix(myCorpus,control = list(minWordLength = 1))
dtm_tfxidf <- weightTfIdf(dtm)
m1 <- as.matrix(dtm_tfxidf)
m<-t(m1)
rownames(m) <- 1:nrow(m)
norm_eucl <- function(m) m/apply(m, MARGIN=1, FUN=function(x) sum(x^2)^.5)
m_norm <- norm_eucl(m)
num_cluster<-6
cl <- kmeans(m_norm, num_cluster)
round(cl$centers, digits = 1)
for (i in 1:num_cluster) {
cat(paste("cluster ", i, ": ", sep = ""))
s <- sort(cl$centers[i, ], decreasing = T)
cat(names(s)[1:5], "\n")
}

OUTPUT

Advantages to Using this Technique
•  With a large number of variables, K-Means may be computationally faster than hierarchical clustering (if K is small).
•  K-Means may produce tighter clusters than hierarchical clustering, especially if the clusters are globular.

Disadvantages to Using this Technique
• Difficulty in comparing quality of the clusters produced (e.g. for different initial  partitions or values of K affect outcome).
• Fixed number of clusters can make it difficult to predict what K should be.
• Does not work well with non-globular clusters.
• Different initial partitions can result in different final clusters. It is helpful to rerun the program using the same as well as different K values, to compare the results achieved.

Applications of K-mean clustering
There are a lot of applications of the K-mean clustering, range from unsupervised learning of neural network, Pattern recognition, Classification analysis, Artificial intelligent, image processing, machine vision, etc. In principle, you have several objects and each object have several attributes and you want to classify the objects based on the attributes, then you can apply this algorithm

References
1) http://home.deib.polimi.it/matteucc/Clustering/tutorial_html/kmeans.html
2) http://croce.ggf.br/dados/K%20mean%20Clustering1.pdf
3) http://www.r-bloggers.com/text-mining-in-r-automatic-categorization-of-wikipedia-articles/
4) http://www.mathworks.com/matlabcentral/fileexchange/screenshots/6432/original.jpg